Derivajo

En matematiko, la derivajo di funciono en punto es la signata mezuro dil rapideso a qua ta funciono chanjas kande sua varianto chanjas. Por funcioni kun multa varianti, on dicas dil partala derivajo per raporto a l’un di sua varianti.

Sur la grafo di la funciono, to korespondas a sua inklineso en ta punto.

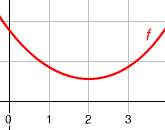
En l'exemplo apuda: en 0, la kurvo decensas, do la derivajo y es negativa (ol valoras -1) en 1, la kurvo decensas sempre, ma l'inklineso esas mikra (-0,5). en 2, la kurvo es perfekte horizontala, do la derivajo es nula (0). en 3, la kurvo acensas, do la derivajo esas pozitiva (0,5).

Formala defino

Sive $f$ reala funciono kun reala valori.

On apelas procento di augmento di $f$ en $x_{0}$ la quanto :

$t_{x_{0}}(h)={f(x_{0}+h)-f(x_{0}) \over h}$

Kad $t_{x_{0}}(h)$ havas limito kande $h$ tendencas vers 0, on dicas ke $f$ es derivebla en $x_{0}$, e sua derivajo egalesas la limito di ta procento ce di augmento. On notas lore :

$f'(x_{0})=\lim _{h\to 0}t_{x_{0}}(h)=\lim _{h\to 0}{f(x_{0}+h)-f(x_{0}) \over h}$

Funciono per qua la derivajo existas en punto es dicinta derivebla en ta punto.

Ta kalkulo di limito rivenas grafike a riserchar la tangento di la kurvo en ta punto. Do, la derivajo di funciono en punto, se ol existas, egalesas la inklineso di la tangento a grafo di la funciono en ta punto.

La derivajo povas anke esar definita sur da funcioni altra ke reala a reala valori.

Exemple, reala funciono $f$ kun valori en $\mathbb {R} ^{n}$, es derivebla en $x_{0}$ se e sole se omna sua koordinati es derivebla en $x_{0}$ ; e sua derivajo es la funciono do la koordinati es la derivadi di koordinati di $f$.

Funciono derivajo

La derivadala es ante locala nociono (derivadala en punto), ma se funciono es derivebla sur omna intervalo, on povas definar sua derivadala funciono sur l'intervalo en questiono. La derivadala funciono, notita $f'\,$ (pronuncita « f prime ») o ${\frac {df}{dx}}$, mantenas en tota punti la valoro dil derivajo di $f\,$ en ta punto.

Funciono egala a sua derivajo es nomizita exponentala funciono.

$f'(x)\,$ povas facile kalkular su de expresiono $f(x)\,$ uzanta mikra nombro di algebrala normi deduktita dil defino donita ante. La normi plu ordinare uzata esas:

Nomo	Normi	Kondicioni
Lineara	$(af+bg)^{\prime }=af'+bg'$	Kelka sive la derivebla funcioni $f\,$ e $g\,$ e la reali a e b.
Potenco	$(f^{\alpha })^{\prime }=\alpha f^{\alpha -1}f'$	Kelka sive $\alpha \in \mathbb {Z}$, e mem kelka sive $\alpha \in \mathbb {R}$ se f es pozitiva
Produto	$(fg)^{\prime }=f'g+fg'$	Kelka sive la derivebla funcioni $f\,$ et $g\,$
Quociento	$\left({f \over g}\right)'={f'g-fg' \over g^{2}}$	Kelka sive la derivebla funcioni $f\,$ e la derivebla funcioni $g\,$ ne nihila
Radiko	$\left({\sqrt {f}}\right)'={f' \over 2{\sqrt {f}}}$	Kelka sive la derivebla funcioni $f\,$ strikte pozitiva
kompozita	$(f\circ g)'=(f'\circ g)\cdot g'$	Kelka sive la derivebla funcioni $f\,$ e $g\,$

derivajo di ordinara funcioni

derivajo di funcioni potenco, log, exp

Funcioni	Derivadi	Kondicioni
$a\,\!$	$0\,\!$
$ax\,\!$	$a\,\!$	$x\,\in \mathbb {R}$
$ax^{n}\,\!$	$anx^{n-1}\,\!$	$n\,\in \mathbb {Z} \quad x\,\in \mathbb {R} ^{*}$
$e^{f}\,\!$	$f'e^{f}\,\!$	$f\,\!$ derivebla
$a^{x}\,\!$	$a^{x}\ln a\,\!$	$a\,\in \mathbb {R} _{+}^{*}\quad x\,\in \mathbb {R}$
$\ln |x|\,\!$	$1 \over x\,\!$	$x\,\in \mathbb {R} ^{*}$

Derivadi des trigonometrika funcioni

• Se $f(x)=\sin(x)\,$ alors $f'(x)=\cos(x)\,$

Demonstro :

$f'(x)=\lim _{x\to a}{\sin(x)-\sin(a) \over x-a}$

$x=a+b\,$

$f'(x)=\lim _{b\to 0}{\sin(a+b)-\sin(a) \over (a+b)-a}$

$f'(x)=\lim _{b\to 0}{\sin(a)\cdot \cos(b)+\sin(b)\cdot \cos(a)-\sin(a) \over b}$

$f'(x)=\lim _{b\to 0}\sin(a){\cos(b)-1 \over b}+\cos(a)\cdot {\sin(b) \over b}$

$\lim _{b\to 0}{\cos(b)-1 \over b}=0$

$\lim _{b\to 0}{\sin(b) \over b}=1$

$f'(x)=\cos(a)\,$

• Se $f(x)=\cos(x)\,$ alors $f'(x)=-\sin(x)\,$

Demonstro :

$f(x)=-\sin(a)\,$

$f'(x)=\lim _{x\to a}{\cos(x)-\cos(a) \over x-a}$

$x=a+b\,$

$f'(x)=\lim _{b\to 0}{\cos(a+b)-\cos(a) \over (a+b)-a}$

$f'(x)=\lim _{b\to 0}{\cos(a)\cdot \cos(b)-\sin(a)\cdot \sin(b)-\cos(a) \over b}$

$f'(x)=\lim _{b\to 0}\cos(a){\cos(b)-1 \over b}-\sin(a)\cdot {\sin(b) \over b}$

$\lim _{b\to 0}{\cos(b)-1 \over b}=0$

$\lim _{b\to 0}{\sin(b) \over b}=1$

$f'(x)=-\sin(a)\,$

• Se $f(x)=\tan(x)\,$ alors $f'(x)=\sec ^{2}(x)\,$

Demonstro :

• Se $f(x)=\operatorname {cotan} (x)\,$ alors $f'(x)=-\operatorname {cosec} ^{2}(x)\,$

Demonstro :

• Se $f(x)=\sec(x)\,$ alors $f'(x)=\sec(x)\cdot \tan(x)\,$

Demonstro :

• Se $f(x)=\operatorname {cosec} (x)\,$ lore $f'(x)=-\operatorname {cosec} (x)\cdot \operatorname {cotan} (x)\,$

Derivadi dil inverso di trigonometrika funciono

• Se $f(x)=\arcsin(x)\,$, lore $f'(x)={1 \over {\sqrt {1-x^{2}}}}$
• Se $f(x)=\arcsin(\varphi (x))\,$, lore $f'(x)={\phi '(x) \over {\sqrt {1-\phi (x)^{2}}}}$
• Se $f(x)=\arccos(x)\,$, lore $f'(x)={-1 \over {\sqrt {1-x^{2}}}}$
• Se $f(x)=\arccos(\varphi (x))\,$, lore $f'(x)={-\phi '(x) \over {\sqrt {1-\phi (x)^{2}}}}$
• Se $f(x)=\arctan(x)\,$, lore $f'(x)={1 \over {1+x^{2}}}$
• Se $f(x)=\arctan(\varphi (x))\,$, lore $f'(x)={\phi '(x) \over {1+\phi (x)^{2}}}$

derivajo di ordino n

On definas la derivajo di ordino $n$ per funciono $n$ foye derivebla per rekurenta:

${\frac {d^{n+1}f}{dx^{n+1}}}={\frac {d}{dx}}{\frac {d^{n}f}{dx^{n}}}$

${\frac {d^{n}f}{dx^{n}}}$ es egale notita $f^{(n)}$.

formulizo di Leibniz

Se $f,g$ esas de la funcioni $n$ foye derivebla, lore :

$(fg)^{(n)}=\sum _{k=0}^{n}{n \choose k}f^{(k)}g^{(n-k)}$.

En partikulara per $n=2$,

$(fg)''=f''g+2f'g'+fg''\,\!$.

Notez la notinda analogeso kun la formulizo pri la binomio di Newton.

Analiso di funciono derivajo

Trovinta la valori di x ube derivajo valas 0 o ne existas, trovesas la krizala nombri di la funciono. La krizala nombro di f posibligas trovar implicite sua maximi e sua minimi. A efektigar la testo dil prima derivajo, on konstruktas tabelo di varianto ; se la signalilo di la funciono derivajo pasas di plu a min ante krizala nombro, on havas maximo e se la signalilo di la funciono derivajo pasas di min a plu ante la krizala nombro, on havas minimo. Pluse, kande la signalilo dil prima derivajo es pozitiva, la funciono acensas ; se ol es negativa, ol decensas. On ne konkluzas nulo se a krizala punto la funciono ne chanjas lua signalilo. En derivadinta la prima derivajo, on havas la duesma derivajo. A efektigar la testo dil duesma derivajo, trovesas la krizala nombri dil prima derivajo per lokizar en mem tabelo ; kande on observas chanjeso di signalilo dil duesma derivajo ante to krizala nombro o nombri, on dicas ke on havas un (o di) punto di inflexo. La punto di inflexo markizas chanjeso dil konkaveso di la funciono derivajo. Pozitiva signalilo dil duesma derivajo signifikas ke la funciono es konkava adsupre e negativa signalilo dil duesma derivajo signifikas ke la funciono es konkava adinfre.

Kande konocesas la chanji en la konkaveso e l'extremi di la funcioni, do on povas trovar skiso di grafiko.

derivajo ed optimiseso

Metodo por maxim bone uzar rendimento per helpo di diferenciala kalkulo:

1ma - Matematikala

a) Defini e desegno : on definas la ne-konocata varianti ed on reprezentas li sur skemo.

b) Skribas la objektala funciono a du varianti e precizigar se on riserchas maximo o minimo en la donita situo.

c) trovar la relato inter la du varianti.

d) Skribas la objektala funciono a un varianto e precizigar la domeno di la funciono.

2ma - Analiso.

a) Derivar la funciono por obtenar la prima derivajo.

b) trovar la krizala nombri di la funciono, ube la prima derivajo valas zero o ne existas en la intervali di domeno.

c) Efektigar la testo dil prima derivajo o la testo dil duesma derivajo por determinar la maximo o la minimo dil situo.

3ma - On formulizas la respondo di konciza fasono por raporto a la questiono.

Derivadi ed asimptoti

Precipua artiklo: Asimptoto

Tanta foye kam on determinas l'asimptoti di la funciono, on povas notar li en la tabelo di varieso por trasar adequate la skiso dil grafiko.