Quadratala equaciono

Grafiko di quadratala funciono:
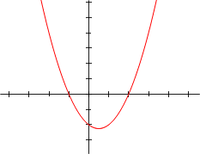
y = x² - x - 2 = (x+1)(x-2)

La x-koordinati dil punti ube la grafiko tra-iras la x-axis, x = -1 e x = 2, es la radiki di quadratala equaciono: x² - x - 2 = 0.

En matematiko, quadratala equaciono esas polinomiala equaciono di duesma grado. Generala formo esas

$ax^{2}+bx+c=0{\mbox{ ube }}a\neq 0.$

La letri a, b e c es nominita koeficienti: a esas la koeficiento di x², b esas la koeficiento di x, e c es la konstanta koeficiento, anke nominita la libera termo.

Quadratala equaciono kun reala o komplexa koeficienti havas du komplexa radiko (i.e., solvi per x kande y=0) kustumala indikita kom $x_{1}$ e $x_{2}$, quankam la du radiki povas esar egala. Ta radiki povas esar kalkulita uzinta quadratala formulo.

Plu alta grado equacioni povas esar quadratala en formo, kom :

$2x^{6}+3x^{3}+5=0$.

Notez ke la plu alta exponento es duopla la exponent-valoro di mezo termo. Ta equaciono povas esar solvita direte o kun simpla substituco, uzinta la metodi ke esas disponebla per quadratala, kom faktoreso, quadratala formulo, o kompleta quadrato.

Quadratala formulo

Quadratala formulo explicite donas la solvi di quadratala equaciono segun la koeficienti a, b e c, qua ni tempe asumar esar reala nombro (ma videz infra per ordinare) kun a esinta ne-zero. Ta solvi esas anke nominita radiko di equaciono. La formulo lektas

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}.$

Alternativa formo existanta esas

$x_{1,2}={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac\ }}}}.$

Exemplo

Exemple $8x^{2}+10x-33=0$. En ta exemplo, 8 esas la koeficiento di x2, 10 esas la koeficiento di x, e -33 esas la libera termo, tale $a=8$, $b=10$ e $c=-33$. Per solva per radiko di equaciono, ni kalkulas $x_{1,2}={\frac {-(10)\pm {\sqrt {(10)^{2}-4(8)(-33)\ }}}{2(8)}}$ To donas la solvi $x_{1}=3/2$ e $x_{2}=-11/4$.

La termo b² − 4ac esas nominita diskriminanto di la quadratala equaciono, per ke inter tri qualiteso altra kazi:

• se la diskriminanto esas zero lore to esas itera solvo x, e ta solvo esas reala. Geometrala, to signifikas ke la parabolo trasita da quadratala equaciono tushas x-axo en solo punto.
• se la diskriminanto es pozitiva, lore to esas du diferanta solvi x, amba reala. Geometrala, to signifikas ke la parabolo trasita da quadratala equaciono tushas x-axo en du punti. Plu, se la diskriminanto esas perfekta quadrato, la radiki esas racionala nombri -- en altra kazi to povas esar quadratala neracionala.
• se la diskriminanto es negativa, lore to esas du diferanta solvi x, amba komplexa nombri. La du solvi esas komplexa konjugi di uno altro. En ta kazo, la parabola ne intersektas x-axo.